Understanding the Difference Between Relations and Functions
This post was last updated on December 9th, 2024
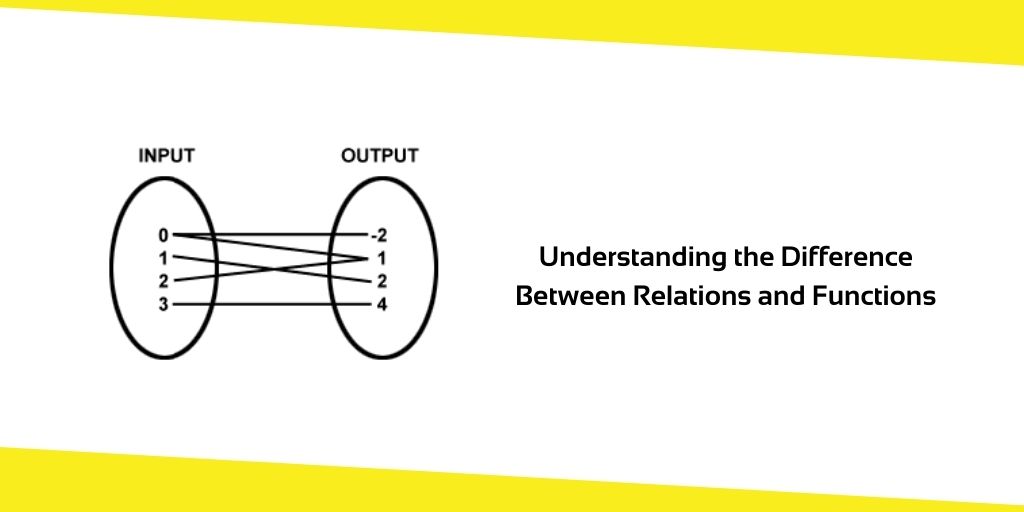
It’s important to remember that functions and relations are inextricably linked and can’t be separated. To distinguish between relations and functions, you must have a thorough understanding of the concepts involved. We’ll use the terms ‘relations’ and ‘functions’ interchangeably throughout this topic to distinguish between Relation and Functions.
What is Relation?
The term ‘relation’ is defined as follows: Any method can connect two or more sets in relational algebra. Consider the following example. Between two sets, A and B, each containing m items and n elements, a connection with any ordered pair that illustrates a relation between them can be quickly established.
In mathematics, a non-empty connection between the elements of two or more sets is referred to as a Relation. A relation ‘R’ is built using a Cartesian product of subsets. If we have two sets and a connection between the items of two or more non-empty sets, for example, the only relationship between the components of the sets in question.
What is Function?
A collection of inputs can be connected to a single output if a relation has the same range mapped to it as a Function. The word ‘function’ is used to describe the connection between the two such that there is only one output for each input.
If you want to think about ordered pairs, an ordered pair is a form of relation or collection of ordered pairs that follow the rule that every value of x should be associated with only one value of y. In most cases, this is referred to as a function.
Consider the following example. The sets A and B are connected in this case. Set A’s elements are related to exactly one member of set B, or any of the components of the given set A is related to an aspect of the provided set B. The use of functions is how this type of relationship is described.
As a result, there is no one-to-many relation between sets A and B when a specific function is used in a particular context.
Note on Functions and Relations –
There are three methods to choose from when describing a relation in mathematics:
- Roster Form – On the surface, a roster form represents a set that lists all of the items currently contained within it. Commas are used to separate entities, and the list is enclosed in brackets.
- Set- builder Form – It is common to use a shorthand approach to writing sets to save time, especially when writing sets with unlimited components. It can be applied to a wide range of other types of numbers in addition to integers and real numbers.
It is also possible to represent sets in the set-builder form using an interval or an equation.
- By Arrow Diagram – The relationship between sets is expressed using the arrow diagram approach, which involves drawing arrows from each pair’s first component to its second component, as long as both features are members of the relationship.
Different Types of Relations in Mathematics
In mathematics, various types of relationships distinguish between Relation and Functions –
There are eight different types of relations. (Please keep in mind that all functions are relations, but not the other way around.)
- Empty Relation – If we choose, we may put R = ∅ as an open Relation.
- Universal Relation – Every element in set A connects with every element in set B, just as a Full relation has a relationship with every aspect in set B. A trivial relation is both empty and universal, and it may be either.
- Identity Relation – A connection is called an identity relation if every member of set A is linked to the same other elements.
- Inverse Relation – Assume we have an R relation between sets A and B, represented by R∈ A×B. Then the inverse relation of R can be written as R -1 = {(b, a) : (a, b) ∈ R}.
- Reflexive Relation – If every element in set A maps to itself set A is referred to as a reflexive relationship.
- Symmetric Relation – R’s relation on a set A is symmetric, if (a, b) ∈R then (b, a) ∈R, such that for all a and b ∈A.
- Transitive Relation – A transitive relationship in a set A is defined as (a, b) ∈R, (b, c) ∈R, and (a, c) ∈R such that for each a, b, c ∈A.
- Equivalence Relation – If and only if all three of these qualities are fulfilled, an equivalence relation is characterised as transitive, symmetrical, and reflexive.
Different Types of Functions in Mathematics
The following are the sorts of functions that may be defined in terms of relationships:
- One to One Function: Take a look at the following function f: A (If there is a distinct value of) B for each value of A in the function, it is said to be One to One. In some circles, the one-to-one function is also known as the Injective function.
- Many to One Function: Many functions map two or more elements from set A to the same element in set B.
- Onto Function: It is referred to as the Onto Function if for every element in set B there is a matching pre-image in set A. In some circles, the onto function is referred to as the Subjective function.
- One-one and Onto Function: Every element of A is matched with a discrete element of B by the function f, and every element of B has a preimage in A by the function f. This is known as the Bijective function, commonly known as the ‘one-one and ‘onto’ function.
The following are some algebraic special functions:
- Constant Function- As a constant function, f(x) = c can be written.
- Identity Function- The formula for a constant function is f(x) =x, where x stands for constant function.
- Absolute Value Function- The absolute value function f(x) =|x| may be written as f(x) =|x|.
- Inverse Functions- The symbol for an inverse function is f -1, which stands for inverse function (x).
- Linear Functions- The equation f(x) = mx c represents a linear function.
Examine the following to distinguish between Relation and Functions:
| RELATIONS | FUNCTIONS |
| A relation is defined as a link between two or more sets of values or variables. It may also be seen as a subset of the Cartesian product. | According to the mathematical theory of functions, a relation is one in which there is only one output for each input. |
| In most circumstances, the letter ‘R’ symbolises a relationship. | The letters ‘F’ or ‘f’ are often used to represent a function. |
| As we can see from the above example, a function is not a relation. | In mathematics, one may argue that every function is a connection. |
Conclusion
A ‘Relation’ is defined in mathematics as a collection of ordered pairs consisting of an item from one set that belongs to another and vice versa to distinguish between Relation and Functions. In contrast, ‘Functions’ are the connections that define a relationship between a collection of inputs and a set of outputs. Each input in the set X has exactly one output in the set Y and vice versa.
Recommended For You
Is Huler1996 Essay Writing Services Legit?
Most Inside
Most Inside offers high-quality recommendations and valuable updates to enhance all aspects of your life, providing premium guidance and enriching experiences.




